This is the page you can come to when a parent is coming in to check your internet usage.
There are also the Random Facts, Quotes, and Words of the Day Archives from which you can claim educational benefit. And pi.
|
|
Cool Educational Links:
|
Doodle-dood Bad Guys and Trigonometry

How could a Soh-Cah-Toan possibly help you with math?
The answer is: when you're dealing with trigonometric functions!
If you already know what a trigonometric function is, skip down to the bottom of this article.
If you already know how to use Soh-Cah-Toa, then skip this article and go read about something else.
If you already know what a triangle is, good for you! If not, we're not the ones to help you.
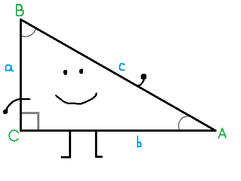
Trigonometric functions deal with the relationships between the angle measures and side lengths in right triangles. A right triangle is a triangle in which one angle is a right angle, meaning it has a measure of 90 degrees (Celsius or Fahrenheit, we'll never know). Below you'll see a picture of a Right Triangle Glub-glub, labeled with two sets of A, B, and C. The capital A, B, and C (in green) label the intersections of the three lines, and also represent the angles formed between the intersecting lines. The lowercase a, b, and c (in blue) label the three lines connecting the three points. The lowercase a, b, and c represent the lengths of the sides of the triangle. You will notice that side a is opposite from angle A, and side b is opposite from angle B, and side c is opposite from angle C. Angle C is the right angle, and side c, the longest side and the side opposite the right angle, is called the hypotenuse.
(Another bit of useful information when dealing with right triangles: Pythagorean theorem- a theorem made by Pythagoras Glub-glub, states that "a" squared plus "b" squared will always equal "c" squared. In other words, if you take the length of the two smaller sides, square them, and add them together, that will always equal the square of the hypotenuse.)
The answer is: when you're dealing with trigonometric functions!
If you already know what a trigonometric function is, skip down to the bottom of this article.
If you already know how to use Soh-Cah-Toa, then skip this article and go read about something else.
If you already know what a triangle is, good for you! If not, we're not the ones to help you.
Trigonometric functions deal with the relationships between the angle measures and side lengths in right triangles. A right triangle is a triangle in which one angle is a right angle, meaning it has a measure of 90 degrees (Celsius or Fahrenheit, we'll never know). Below you'll see a picture of a Right Triangle Glub-glub, labeled with two sets of A, B, and C. The capital A, B, and C (in green) label the intersections of the three lines, and also represent the angles formed between the intersecting lines. The lowercase a, b, and c (in blue) label the three lines connecting the three points. The lowercase a, b, and c represent the lengths of the sides of the triangle. You will notice that side a is opposite from angle A, and side b is opposite from angle B, and side c is opposite from angle C. Angle C is the right angle, and side c, the longest side and the side opposite the right angle, is called the hypotenuse.
(Another bit of useful information when dealing with right triangles: Pythagorean theorem- a theorem made by Pythagoras Glub-glub, states that "a" squared plus "b" squared will always equal "c" squared. In other words, if you take the length of the two smaller sides, square them, and add them together, that will always equal the square of the hypotenuse.)
Now for the trig functions. Trigonometry, by the way, is the study of triangles, and trigonometric functions only work with right triangles, as does Pythagorean theorem, although there are more complicated formulas that let them deal with non-right triangles. The three basic trig functions are known as Sine, Cosine, and Tangent, and are abbreviated sin, cos, and tan. The trig functions are ratios referring to the relationship between the sides and angles of a triangle.
And now for the green, brainless Doodle-doods: what you need to know is SOH-CAH-TOA.
In short, this is how to remember it:
SOH: Sine- Opposite over Hypotenuse
CAH: Cosine- Adjacent over Hypotenuse
TOA: Tangent- Opposite over Adjacent
To get the sine of an angle, divide the length of the opposite side by the length of the hypotenuse. We use the term "over" in "opposite over hypotenuse" to denote division because we write division like a fraction, with one number on top of another, by which the top number is divided.
FOR EXAMPLE: to find the cosine of angle B (cos B), use CAH (Cosine: Adjacent over Hypotenuse). Which side is adjacent? Well, "adjacent" means "next to." The two lines next to angle B are lines a and c. c is the hypotenuse, which is used elsewhere in the equation, so the adjacent line is line a. The hypotenuse is c, so the cos B is adjacent divided by hypotenuse, or a divided by c. Another way to write that:
cos B = a/c
For sine and tangent, you will need to use the opposite side, which is simply the only side not touching the angle.
For example, tan A = a/b
And now for the green, brainless Doodle-doods: what you need to know is SOH-CAH-TOA.
In short, this is how to remember it:
SOH: Sine- Opposite over Hypotenuse
CAH: Cosine- Adjacent over Hypotenuse
TOA: Tangent- Opposite over Adjacent
To get the sine of an angle, divide the length of the opposite side by the length of the hypotenuse. We use the term "over" in "opposite over hypotenuse" to denote division because we write division like a fraction, with one number on top of another, by which the top number is divided.
FOR EXAMPLE: to find the cosine of angle B (cos B), use CAH (Cosine: Adjacent over Hypotenuse). Which side is adjacent? Well, "adjacent" means "next to." The two lines next to angle B are lines a and c. c is the hypotenuse, which is used elsewhere in the equation, so the adjacent line is line a. The hypotenuse is c, so the cos B is adjacent divided by hypotenuse, or a divided by c. Another way to write that:
cos B = a/c
For sine and tangent, you will need to use the opposite side, which is simply the only side not touching the angle.
For example, tan A = a/b
Do not visit this page. The only educational thing you will learn is how much you should not click that link.